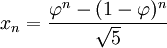Ángulos en el círculo

Al parecer la mayor parte de las dudas giran alrededor de este tema. Antes de iniciar a resolver los

problemas propuestos en el libro de Abelardo Guzmán, hay que aprender a reconocer los diferentes tipos de ángulos que han en un círculo.

Iniciemos con el ángulo central, un ángulo central está formado por dos radios del círculo, se llama central porque su vértice coincide con el centro del círculo.

La característica de este ángulo es que mide lo mismo que el arco comprendido por los dos radios que lo forman.

Así, si el arco BC midiera 85°, el ángulo A que está marcado de color verde en la ilustración de la izquierda, también mediría 85°.

Se le llama ángulo inscrito o semi-inscrito a cualquier ángulo que tenga su vértice sobre la circunferencia, la diferencia entre uno y otro es que los inscritos estan formados por por dos cuerdas, dos secantes o una cuerda y una secante, en la ilustración de la izquierda tenemos un ejemplo de un ángulo inscrito formado por dos cuerdas; por su parte, los ángulos semi-inscritos están formados por una secante una tangente, o una cuerda y una tangente (como el de la ilustración de la derecha), si los vemos gráficamente, en los semi-inscritos se aprecia que una parte del ángulo queda fuera de la circunferencia, por ello el prefijo semi.

Ambos tipos de ángulos tienen la característica de medir la mitad del arco comprendido por los lados del ángulo.

Los ángulos interiores son aquellos ángulos que tienen su vértice, como su nombre lo dice, en el interior de la circunferencia sin que coincida con el centro, pueden estar formados por dos cuerdas, por una cuerda una secante o por dos secantes. La medida de un ángulo interior la calculamos sumando los dos arcos que forman los lados del ángulo interior y dividiendo el resultado de esta suma entre dos.

Existen también los ángulos exteriores, éstos ángulos tienen la característica de que su vértice está fuera del círculo, éstos pueden estar formados por dos secantes (como el de la ilustración de abajo), por dos tangentes o por una secante y una tangente. Si observas, los lados del ángulo exterior delimitan dos arcos, un arco grande (en la ilustración CD es el arco mayor) y un arco mas pequeño (BA en nuestro ejemplo ilustrado). Para calcular la medida de un ángulo exterior, solo debemos restar a la medida del arco mayor la medida del arco menor y este resultado dividirlo entre dos.

Espero que con esta introducción puedan resolver los ejercicios de ángulos que dejamos de tarea. Si quieres ver ejercicios resueltos, puedes consultar:

http://roble.pntic.mec.es/jarran2/cabriweb/circunf/anguloscircun.htm

http://cl.kalipedia.com/matematicas-geometria/tema/circunferencia-circulos/calculo-valor.html?x1=20070926klpmatgeo_146.Kes&x=20070926klpmatgeo_149.Kes

Si deseas manipular un poco algunos ángulos para que te convenzas de la relacion que hay entre los ángulos y los arcos comprendidos por sus lados, puedes visitar:

http://www.dmae.upct.es/~pepemar/angulo/home.htm

http://contenidos.educarex.es/cnice/descartes/Esp/3_eso/capaz_d3/cuerdas.html

http://www.recursos.pnte.cfnavarra.es/~msadaall/geogebra/figuras/an1circunferencia.htm

¿Dudas?

Cómo convertir de grados a radianes y viceversa

Hola,


una de las actividades que hay que realizar para la próxima clase es conversión de radianes a grados y de grados a radianes.

Ya habíamos comentado en clase que ambas son unidades de medida de ángulos, un grado lo definimos como la 360ava parte de una circunferencia y un radián es la medida de un ángulo central cuya longitud del arco y el radio miden lo mismo.

Si recordamos, la relación que hay entre el diámetro y el perímetro de un círculo está definida por el famosísimo número π.

Sabemos también que un diámetro es equivalente a dos radios, por lo que podemos deducir que un radio cabe 2π veces en la circunferencia, de ahí que

2π rad = 360°,

dividiendo por 2 la igualdad obtenemos

π rad = 180°

Esta relación la vamos a usar para hacer conversiones entre radianes y grados mediante una regla de tres.

Hagamos un ejemplo, supongamos que deseamos saber a cuantos radianes equivalen 65°, entonces tenemos lo siguiente:

π rad = 180°

? rad = 65°

Resolviendo la regla de tres tenemos

? rad = ((65°)(π rad))/180°

simplificando la fracción 65/180 tenemos 13/36 (lo obtuvimos dividiendo entre 5 tanto el numerador como el denominador de la fracción orginal), como ya no se puede reducir mas, tenemos que

65° = 13/36 π rad

Observen que los radianes se expresan normalmente en función de π, es decir, como una fracción de π, así por ejemplo, para referirnos a un ángulo de 90° en radianes decimos π /2 rad o lo que es lo mismo 1/2 π rad.

Por el contrario, si queremos convertir 3/4 π rad a grados, nuevamente recurrimos a la regla de tres partiendo de la relación que ya conocemos:

π rad = 180°
3/4 π rad = ?°

Nuevamente resolvemos por medio la regla de tres,

?°=(3/4 π rad)(180°) / π rad

y obtenemos:

?° = 135°

Si hubiera alguna duda sobre el tema no duden en plantearla.

Resuleve el sistema

Bueno, en virtud de que la mayor dificultad está siendo traducir a lenguaje algebraico los problemas planteados con palabras, en lo podemos representar simbólicamente el problema anterior, propongo resuelvan el siguiente sistema para que vayan practicando uno de los métodos que han investigado.

3x + y= 2

8x - 3y = 28

Calcular el valor de x y y.

El rectángulo

Nuevamente les pido que compartan, además de la respuesta, el razonamiento que están empleando para llegar a la solución.

Si la base de un rectángulo disminuye 2 pulgadas y la altura aumenta 2, su área se incrementa en 16 pulgadas cuadradas. Si la base aumenta 5 pulgadas y la altura disminuye 3, el área aumenta 15 pulgadas cuadradas. Encontrar el área del rectángulo original.

¿Cuál es la edad de Beatriz y Guillermo?

Hace seis años Beatriz tenía 2/3 de la edad de Guillermo, y dentro de 12 años tendrá 5/6 de su edad. ¿Qué edad tienen Beatriz y Guillermo en la actualidad?

NOTA: Además de incluir las respuestas, explica el procedimiento que empleas para llegar a las mismas.

Catalina y sus inversiones

Iniciemos ahora con un nuevo tipo de problemas diferentes a los que hemos visto en clase:

Catalina invirtió parte de su dinero al 8% y el resto al 12%. El ingreso obtenido por ambas inversiones totalizó $2 440. Si hubiera intercambiado sus inversiones, el ingreso habría totalizado $2 760. ¿Qué cantidad de dinero había en cada inversión?

Gauss, el príncipe de las Matemáticas

Johann Karl Friedrich Gauss fué un notable físico-matemático alemán que nació en 1777 en el seno de una humilde familia y murió en 1855 a la edad de 77 años. Trabajó en una amplia variedad de campos de matemáticas y física como teoría de números, analisis, geometría diferencial, geodesia, magnetismo, astronomía y óptica. Su trabajo tuvo un gran influencia en muchas áreas. Se le considera "el príncipe de las matemáticas" y "el matemático mas grande desde la antigüedad".

Fué un niño prodigio, se dice que a la edad de 3 años corrigió unos calculos que estaba realizando su padre y que a los 5 años (algunos autores dicen que fue hasta los 7 y otros mas que a los 10) calculó en pocos minutos la suma de los primeros 100 números, tarea que le había encomendado su profesor de primaria para mantenerlo ocupado durante horas, según él.

Para calcular esta suma, a Gauss se le ocurrió que

1+100=2+99=...=50+51

Era claro que la suma era

50x101=5050

Hagamos ejercicios similares al que realizó Gauss en su infancia:

1. Calcula la suma de los primeros 200 números naturales
2. Los 50 primeros números pares
3. Los 100 primeros números impares
4. Los 40 primeros múltiplos de 3
5. Los múltiplos de 5 menores que 180
6. Los primeros 25 múltiplos de 9
7. Los múltiplos de 7 comprendidos entre 22 y 225

¡¡Espero sus resultados!! Recuerden argumentar sus respuestas.

De varios triángulos

Uno más, para ejercitar lo aprendido.

Encuentra AB en la figura, si CD=10 y el ángulo C mide 30°.

Alan y Bárbara

Les dejo un problema no tan trivial como los anteriores:

Alan y Bárbara, quienes están parados a 400m entre sí, arrojan piedras a un blanco que se encuentra cruzando una barranca profunda.

En la figura, dado el triángulo ABC donde el ángulo A mide 35° y el ángulo B mide 55°, Alan está parado en A, Bárbara en B y el blanco al que están tirando se ubica en C.

Encuentra las distancias de Alan y Bárbara al blanco.

Antes que nada un saludo a todos mis compañeros, además les pido una sincera disculpa por no haber publicado esto antes, pero por causas de fuerza mayor y por influencia de la influenza me fue imposible hacerlo.
Bueno aquí les dejo esto y les recomiendo que observen bien los problemas, y en base a los datos disponibles procedan a responderlos según los conocimientos adquiridos y la recopilación de información del tema… bueno suerte y si les puedo ayudar en aclararles alguna duda no duden en preguntarme.
Bye Atte. “YO”

Aquí les dejo mi msn para quien no lo tenga o tenga alguna duda; mis servicios son gratuitos, aplican restricciones.
ivan_rfi_personal@hotmail.com

-----------------------------------------------------------
-Problemas de culturas antiguas que implican el conocimiento de la relación pitagórica.

1 (nr2)
De otra tablilla babilónica:
Uno de los lados de un trapecio es 30, el segundo lado es 30, el ancho superior es 50, el ancho inferior es 14. Halle el área del trapecio.

2 (nr3)
Otro problema que figura en una tablilla babilónica es el siguiente:
Hallar el radio del círculo circunscrito
al triángulo de lados 50, 50 y 60.

3 (nr4)
Otra tablilla, hallada en 1962, perteneciente a un período cercano al 1000 a. C. dice lo siguiente:
Hallar la longitud y la anchura de la figura (rectángulo), dadas su área 0,75 y diagonal 1,25.

4 (nr6)
Una viga de 30 unidades de largo se apoya verticalmente contra un muro; si la extremidad superior de la viga se coloca 6 unidades más abajo, ¿en cuántas unidades se desplazará el otro extremo de la viga?

5 (nr7)
Una escalera de 10 codos está con sus pies a 6 codos de la pared.
¿Qué altura alcanza la escalera?


6 (nr10)
La altura de una puerta excede a su ancho en 6 chih 8 tsun.
La distancia máxima entre sus vértices es 1 chang.
¿Cuál es la altura y cuál es el ancho de la puerta?
(1 chang = 10 chih, 1 chih = 10 tsun )

7 (nr14)
De lo alto de un árbol cuelga una soga con 3 chih de la misma extendidos por el suelo. Cuando la soga se tensa de manera que su punta toque exactamente el suelo alcanza un punto a 8 chih de la base del árbol.
¿Cuál es la longitud de la soga?

8 (nr17)
A ambas orillas de un río hay dos árboles, uno frente al otro. Uno de los árboles tiene una altura de 20 codos, el otro de 30 codos. La distancia entre sus troncos es de 50 codos. En la cima de cada árbol hay un pájaro. De pronto, los dos pájaros ven un pez que aparece en la superficie del agua entre los dos árboles y se lanzan para alcanzarlo. Lo alcanzan al mismo tiempo.
¿A qué distancia del tronco de los árboles apareció el pez?

Decágono regular

Calcular el área de un decágono regular circunscrito a una circunferencia de 5 cm. de radio.

Angulos de la diagonal con los lados del rectángulo

Los lados de un rectángulo miden 21.9 y 29.2 metros, respectivamente. ¿Cuánto mide cada uno de los ángulos que forma la diagonal con los lados del rectángulo?

Con la escalera

¿Qué altura alcanza sobre un muro una escalera de 5 metros de largo, si forma con el piso un ángulo de 65° 10´?

Encuentra la altura de la torre.

Aprovechemos estos días de encierro en casa para practicar resolviendo problemas de los temas que hemos visto en clase.

A 87.5 metros de la base de una torre el ángulo de elevación a su cúspide es de 37° 20´. Si sabemos que la altura del aparato con que se midió el ángulo es de 1.50 metros, ¿cuánto mide la altura de la torre?

LAS CALCULADORAS Y LAS FUNCIONES TRIGONOMÉTRICAS.

Evaluación de funciones trigonométricas con la calculadora

Existen calculadoras programadas para evaluar las funciones trigonométricas. En estas calculadoras encontramos las teclas [SEN], [COS], [TAN]. Estas teclas se usan para evaluar las funciones de coseno, seno y tangente de forma directa. No hay teclas para las funciones cosecante, secante y cotangente. Debido a que:

son identidades recíprocas de sen x, cos x, y tan x, respectivamente, se puede usar la tecla de coseno, seno y tangente, luego oprimir la tecla de la función recíproco:

De esta manera se obtiene csc x, sec x y cot x.

Entonces al momento de utilizar la calculadora sólo calcularemos la función fundamental y con la tecla de inverso obtendremos la función recíproca.

TRIGONOMETRÍA

LA TRIGONOMETRÍA

Iniciaré dando una introducción acerca de que es la trigonometría.
La trigonometía es una rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Para esto se vale de razones trigonométricas, las cuales son utilizadas frecuentemente en cálculos técnicos. En términos generales, la trigonométria es el estudio de las funciones seno, coseno, tangente, cotangente, secante y cosecante.

Ahora ya con este término aclarado, trabajaremos las funciones trigonométricas que son: seno, coseno, tangente, cotangente, secante y cosecante mencionadas ya anteriormente.

Tambien antes de tarabajar con estas funciones es necesario aclarar otros términos estos son:
Hipotenusa:
Es el lado del triángulo rectángulo que enfreta el ángulo recto.
Cateto opuesto:

Es el lado del triángulo rectángulo que enfrenta el ángulo al cuál se le va a calcular la función trigonométrica.
Cateto adyacente:

Es el lado del triángulo rectángulo que junto con la hipotenusa definen el ángulo al cual se le va a calcular la función trigonométrica.

Las funciones trigonométricas son seis pero basicamente son utilizadas tres ya que las otras funciones son recíporicas es decir; que estan funciones son el contrario o el reverso de las otras tres.

Recíproco: Dos cantidades son recíprocas cuando el producto de ellas es 1.
Por lo tanto estas funciones son las siguientes:

Estas son las funciones trigonométricas donde se muestra que son recíprocas ya que son el inverso del seno, coseno y tangente.

Las funciones recíprocas no se deben confundir con las razones inversaa ya que las funciones inversas son las que retroceden el proceso es decir que sólo regrsan la operacion realizada ademas se denominan con el prefijo arco.

y = sin x Inverso x = arcsin y.

y = cos x Inverso x = arccos y

y = tan x Inverso x = arctan y

Estas funciones inversas tambien son expresadas como sen-1, cos-1 y tan-1 en las calculadoras. Pero esto será explicado en las siguiente entrada.

Teorema de Pitágoras

Para poder realizar la próxima actividad de nuestra guía debemos recordar algunos temas de geometría, uno de ellos es el teorema de Pitágoras.

El teorema de Pitágoras se aplica únicamente a triángulos rectángulos (los que tienen un ángulo recto), no funciona con otro tipo de triángulos, eso hay que tenerlo siempre presente.

Cuando tenemos un triángulo rectángulo a los dos lados que forman el ángulo recto se les conoce como catetos y al lado que está enfrente del ángulo recto se le llama hipotenusa.

El teorema de Pitágoras estable la relación que guardan los catetos con respecto a la hipotenusa, es decir, no importa de que tamaño sea el triángulo ni cuales las medidas, si el tríángulo es rectángulo siempre se cumplirá. La relación es la siguiente:

"La suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa"

Generalmente se usan las letras a y b para representar a los catetos y la letra c para representar a la hipotenusa, asi que el teorema de Pitágoras se puede simbolizar como

a²+b²=c²

Podemos encontrar mas información al respecto en las siguiente direcciones:
http://www.appletpie.com/apie/apiedemo/teorema_de_pitagoras.html
http://roble.pntic.mec.es/jarran2/cabriweb/1triangulos/teoremapitagoras.htm
http://www.redmexicana.com/comun/actividadeseducativas/matematicas/Pitagoras/default.asp

Bienvenida

Estimados estudiantes,

lo prometido es deuda, iniciamos ahora con este nuevo espacio para reforzar lo visto en el aula de nuestro curso Matemática y Vida Cotidiana II.

A manera de prueba, para ver si les llega la invitación al blog, les dejo la dirección de una página que me ha parecido puede ayudarnos a reforzar lo que vimos en el proyecto anterior relativo a sucesiones y series. La dirección es http://www.disfrutalasmatematicas.com/algebra/sucesiones-series.html

Recuerdo que una de las cosas que quedó pendiente en clase era encontrar la regla con la que pudieramos calcular el término enésimo de la sucesión de Fibonacci, en esa página la podrán encontrar, la regla es
Con esta regla entonces podemos calcular el término que queramos de la sucesión sin tener que calcular todos los términos anteriores.

Bienvenidos nuevamente, y seguimos con el proyecto de Geometría.